MY Cover Letter
Mathematicians
and physicists, in particular, are well aware that a large
number of
"positive qualities" in
this
world are connected to each other. The author of this
submission states
that exactly the same happens with the number 3.
The author reminds that stable orbits exist only in a
three-dimensional space.
Yes, 3D space has a strange property: any perturbation
leads to a NEW
stable orbit.
This
phenomenon can be
described by corresponding solutions for the motion of a
point charge in a Coulomb field in 3D space. There are no
similar equations in other
realms of mathematics that manifest such an amazing
property as those
describing the motion in 3D space.
The author
can give some other example.
Let us ask
ourselves, in how many dimensions can one find the
vector product with
good properties. The answer is simple - only in three
dimensions. In two or
four dimensions there is no vector product at all!
Therefore, it is impossible
to introduce the correct concept of the rotor,
furthermore, the vector algebra
simply does not exist in these dimensions.
We can
continue to bring more examples.
Yet, the author
decided to go ahead.
He only asks
the question: is there some other property
that would have tied
these two seemingly different concepts such as
ordinary N-dimensional
space with its Newtonian (or Descartes?) mechanics, and
number 3.
The author used the help of a home computer in solving
this question and he
obtained an interesting answer. It turns out that there is
a link and this link
can be established through a very interesting mathematical
object. The author
calls it s the Invariant of a Precise Filling.
Main article
download pdf
|
Illustrative program of
the article "X-problem of number 3. Definition
..."
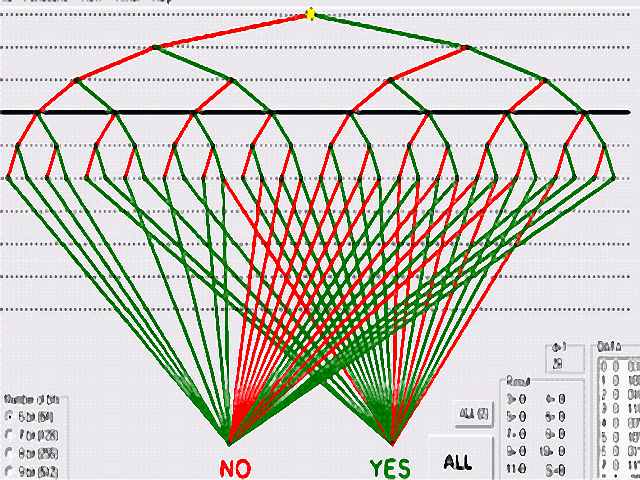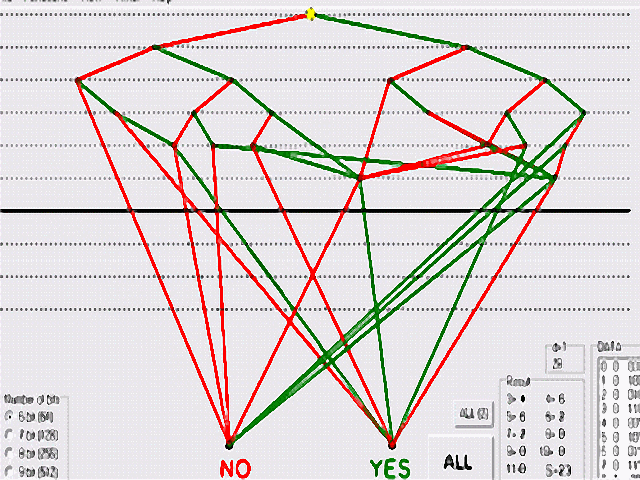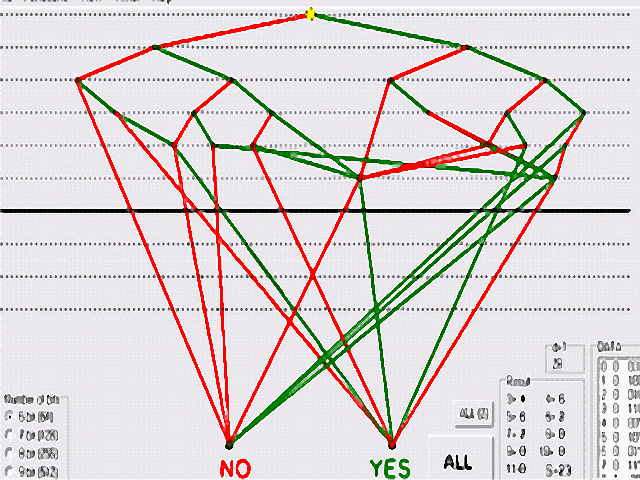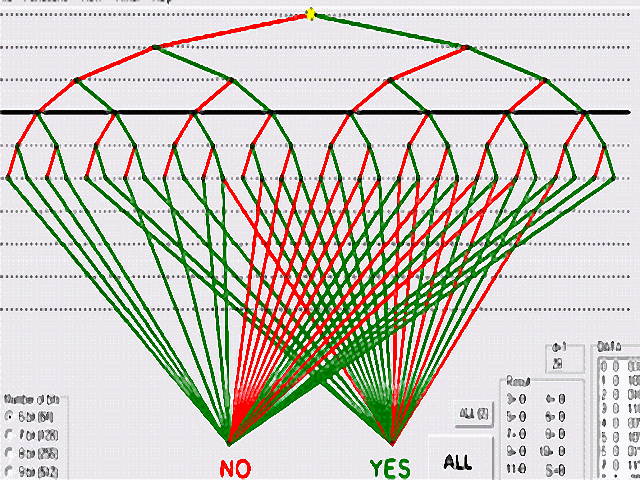
The program can calculate the value Cr
for any mask.
1). Start the demonstration. Download the program illustr_prg.zip, unzip, and run illustr_prg.exe. Press button "Start test" (no. 1 in the figure). The program will be calculate the value Cr for mask (2,1). (The mask is located in the upper right corner) (next) download zip illustr_prg_e.zip |
1. X-problem of integer 3 |
 |