Bсе солитоны в "одном флаконе"
Аннотация Представлено, простейшее уравнение, зависящее только от коэффициентов квадратного трёхчлена, которое даёт, по видимому, практически все известные "виды" солитонов: аналог КдФ уравнения, самодвижущаяся "палочка" с Законом Сохранения, самодвижущаяся "палочка" без(!) с Закона Сохранения, все эти солитоны в "тёмновом" варианте, эффект нелинейной самофокусировки и пр. пр. Всё реализовано в виде демонстрационной программы.
© Корнюхин Александр Фёдорович
1. Введение
Всем известно, что
исследование Интегрируемых Систем (солитонов) составляет
значительную часть Математической Науки. На этот счёт
существуют даже свои энциклопедии [1]. Но представляет
интерес, хотя бы из педагогических целей, найти некий
"наипростейший" солитон, который стоит в самом основании.
Кажется, это не сложно сделать!
По мнению автора, начинать изложение Теории Солитонов с уравнения Кортевега - де Фриза [2] - это неправильно. Ну, да! Для него существует красивое и точное двух- частичное решение. Но что это даёт для понимания? Гораздо правильнее, на мой взгляд, начинать с моих шагающих "Солитонных Палочек с Законом Сохранения". Строить для неё преобразование Берклунда, и... идти дальше.
Дело в том, что почти все известные типы солитонов вытекают, если брать различные коэффициенты (a, b, с) обычного квадратного двучлена: aY2+bY+c в нашей несложной формуле. (На самом деле, независимых коэффициентов - два. Можно выполнить ни на что не влияющие преобразование Z = kY и мы придём к выводу, что коэффициент а можно умножить на k2, а коэффициент b на k, где k - любое. Но если мы хотим, чтобы наши решения оставались в промежутке 10-2 - 102, и хотим, чтобы наши примеры существенно менялись за один- десять шагов, то лучше оставить все три коэффициента).
Сначала нужно скачать программу. www.kornju.narod.ru/All_sol.exe .
Пользоваться ей очень легко! (Запустите её, потом нажмите соответствующий "Hit", а потом "Go").
2. Описание
программы "Все солитоны в одном флаконе"
Мы рассматриваем функцию y(t)
на одномерной решётке замкнутой в кольцо. Закон изменения в
следующий момент времени даётся формулой:
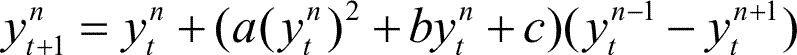
(n - номер- координата соответствующей решётки), при условии

Это условие очень важно! Если его отключить (можно сделать в программе) то ничего не работает. График y(t) либо "застывают", либо уходит на бесконечность. Убедитесь в этом сами.
Посмотрим теперь на саму программу. В ней, с самого начала, предлагается нажать на кнопку Hit на соответствующей цветной панельке, а потом нажать кнопку Go. Программа заработает... И для начала по-пережимать их все.
Кнопка Hit выбирает, во первых, (1). коэффициенты a, b, с в уравнении. (Здесь возможны два варианта. Условно, когда коэффициент c очень мал или нет. В случае если он очень мал, он задаётся в виде e-k, где k - целое).
И, во вторых, (2) задаёт начальные условия. (Здесь тоже возможны два варианта. Можно задать какую то часть точек y случайными числами от 0 до А. А можно можно задать до шести первоначальных точек y. Все остальные значения, в таком случае, ноль).
Теперь о наших параметрах.
В самом верху полное количество точек. (По умолчанию - 30).
Параметры панели MANAGE: общее количество шагов (Nsteps), через какое число шагов происходит остановка (N_fini), через сколько шагов выводится изображение (Speed), задержка после любого шага delay в миллисекундах (поставьте значение 500, и программа будет делать лишь два шага в секунду), и последнее: (*_) = коэффициент домножения графика на экране. Если он равен 100, то значение ординаты совпадает со значением на экране 1 - 2.8.
Кнопки обозначенные "<>" означают увеличение или уменьшение или увеличение данной величины (коэффициента, начальной амплитуды) на 1.1 или 1.01. "-" - изменение знака.
Справа внизу - суммарный график всех y от числа шагов (времени, t). Слева внизу текущие (первые 30) значения y,
Для самостоятельной работы, если хотите найти свой, "новый" солитон, нужно нажать на какой-то "Hit" (выбрать приблизительные условия), а потом изменить коэффициенты a, b, с (значками "-", "<", ">", "D=0" (эта кнопка делает данный коэффициент таким, чтобы дискриминант стал равен 0).
Потом выбрать начальные условия. Для этого выбираем нужные параметры и нажимаем кнопку "DO". (Кнопка "Add" под ней не делает, как кнопка DO, вначале, все значения равными 0, а только добавляет выбранное). И запускаем программу. Смотрим, что получилось...
Разберём кратко все наши кнопки "Hit".
I. Очень интересный пример самофокусировки. Кластер из трети (первых 10 из 30) первоначальных случайных значений переходят в 2 - 4 четыре, совершенно одинаковых, сфокусированных пучка. Каждый пучок через три шага повторяется, но смещается на две позиции вправо. Рис 2.1.
II. Солитонные Палочки без(!) Закона Сохранения. (Говорим что Закон Сохранения существует, если сумма всех y(t) приблизительно постоянна). "Солитонные Палочки" появляются прямо "из нуля", смещаясь при этом на одну позицию. Как водится, скорость движения Палочки возрастает с амплитудой. Палочки проходят друг через друга... но всего лишь несколько раз. (Каждый раз, при проходе, обе амплитуды слегка подравниваются. А когда они сравняются, Палочки идут уже синхронно). Рис 2.2.
III. Две солитонные Палочки с Законом Сохранения. (По моему мнению, это и есть первичный солитон). Если их амплитуды отличаются не сильно, то та которая по- больше не может перепрыгнуть ту которую по- меньше, и они так и идут, одна за другой. (А меняется ли, скорость первой палочки, когда её подгоняют? Догадайтесь... Ответ: "нет", не меняется! Она как шла, так и идёт, шаг в шаг! Нажмите сначала в кнопку "t1", а потом кнопку "t2" и убедитесь. (Надо будет подождать немножко, пока Палочка не достигнет координаты n=25).
IV. Шесть разных (существенно отличающихся по амплитуде) Палочек с Законом Сохранения. Палочка амплитуды 2 может проходить через Палочку амплитуды 1 сотни и сотни раз без существенного изменения амплитуд. Рис 2.3. Панель А[6] здесь же даёт шесть максимальных амплитуд, если брать три точки подряд. (Сначала определяется максимальная амплитуда. Потом эти точки выкидываются, и берутся три следующие... и так далее). Позволяет проследить, как "маленькие" солитоны "давятся большими".
Кнопка "s" ещё сначала сглаживает наши палочки. Это приводит к тому, что самая большая палочка начинает буквально "носится" по полю, перепрыгивая через другие солитоны.
V. Аналог КдФ уравнения. Хорошо вино, что оно, всё-таки, вторично по отношению к нашей Палочке из предыдущего пункта. Рис 2.4.
VI. Темновые "нестабильные" солитоны. Рис 2.5. Кнопки "+" и "-" дают по два два "чистых" тёмновых солитона. (Чтобы показать их прохождение друг сквозь друга). Особенно интересен второй случай! Тёмновой, отрицательный" солитон. Идёт в ДРУГУЮ СТОРОНУ!!! И тоже, естественно, проходит "друг сквозь друга"!
VII. Те же "темновые солитоны", но с очень быстрым остыванием.
VIII. Солитоны с разными амплитудами, идут с практически равными скоростями. (Солитонные пакеты). Рис 2.6.
Меняйте в программе коэффициенты a, b.с, параметры, выбирайте другие начальные условия и ищите новые солитоны. Странно, что я не встретил буквально- ТАКОГО солитона в литературе. Даже в энциклопедии [1] его нет? Что странно! "Палочка с Законом Сохранения" - по моему, очень красивая и интересная вещь.
Подменю главного меню "Exploring part" позволяет сделать постоянную подложку (для темновых солитонов), и сгладить наши y-ки. Один или сто раз.
Особая часть: Японские клеточные солитоны. (Я их назвал так, потому что их первыми исследовали японские математики[3]. По другому их называют "Система Ящиков Шаров". В ней шары сначала нумеруются по возрастанию (слева на право), а потом перекладываются: каждый на ПЕРВОЕ СВОБОДНОЕ место справа.
Выберите в главном меню Jap. works -> Have cell. solitons -> Go
Литература:
[1] Энциклопедия Интегрируемых Систем. 2007, 2008 Институт Теоретической Физики. Редакция: А. Б. Шабат и другие...
[2] Дж. Л. Лэм. Введение в теорию солитонов. Москва "Мир" 1983
По мнению автора, начинать изложение Теории Солитонов с уравнения Кортевега - де Фриза [2] - это неправильно. Ну, да! Для него существует красивое и точное двух- частичное решение. Но что это даёт для понимания? Гораздо правильнее, на мой взгляд, начинать с моих шагающих "Солитонных Палочек с Законом Сохранения". Строить для неё преобразование Берклунда, и... идти дальше.
Дело в том, что почти все известные типы солитонов вытекают, если брать различные коэффициенты (a, b, с) обычного квадратного двучлена: aY2+bY+c в нашей несложной формуле. (На самом деле, независимых коэффициентов - два. Можно выполнить ни на что не влияющие преобразование Z = kY и мы придём к выводу, что коэффициент а можно умножить на k2, а коэффициент b на k, где k - любое. Но если мы хотим, чтобы наши решения оставались в промежутке 10-2 - 102, и хотим, чтобы наши примеры существенно менялись за один- десять шагов, то лучше оставить все три коэффициента).
Сначала нужно скачать программу. www.kornju.narod.ru/All_sol.exe .
Пользоваться ей очень легко! (Запустите её, потом нажмите соответствующий "Hit", а потом "Go").
2. Описание
программы "Все солитоны в одном флаконе"
Мы рассматриваем функцию y(t)
на одномерной решётке замкнутой в кольцо. Закон изменения в
следующий момент времени даётся формулой: 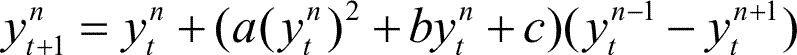
(n - номер- координата соответствующей решётки), при условии

Это условие очень важно! Если его отключить (можно сделать в программе) то ничего не работает. График y(t) либо "застывают", либо уходит на бесконечность. Убедитесь в этом сами.

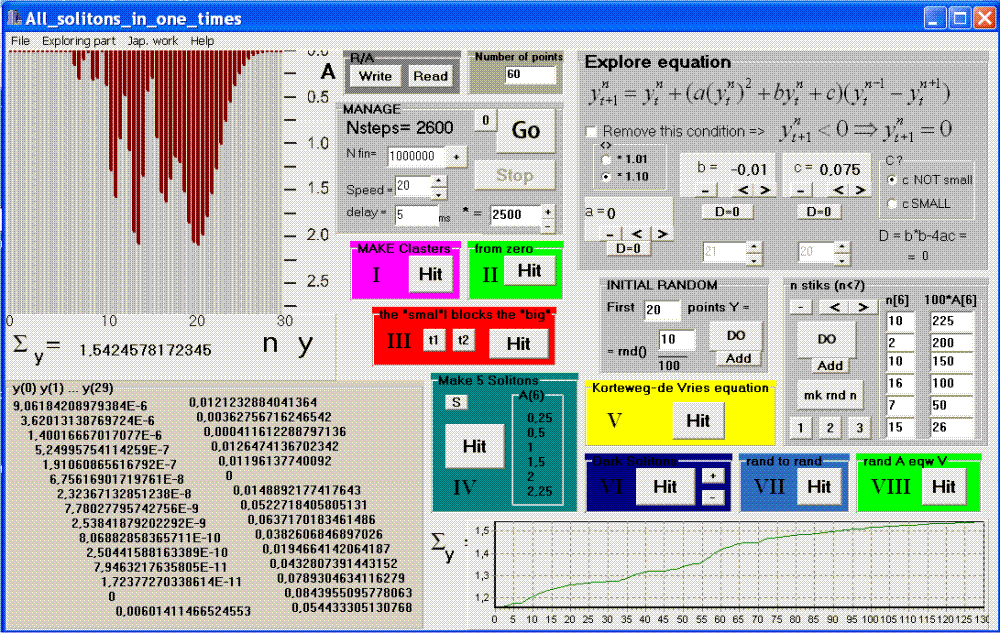
Рис. 1. Внешний вид
программы.
Посмотрим теперь на саму программу. В ней, с самого начала, предлагается нажать на кнопку Hit на соответствующей цветной панельке, а потом нажать кнопку Go. Программа заработает... И для начала по-пережимать их все.
Кнопка Hit выбирает, во первых, (1). коэффициенты a, b, с в уравнении. (Здесь возможны два варианта. Условно, когда коэффициент c очень мал или нет. В случае если он очень мал, он задаётся в виде e-k, где k - целое).
И, во вторых, (2) задаёт начальные условия. (Здесь тоже возможны два варианта. Можно задать какую то часть точек y случайными числами от 0 до А. А можно можно задать до шести первоначальных точек y. Все остальные значения, в таком случае, ноль).
Теперь о наших параметрах.
В самом верху полное количество точек. (По умолчанию - 30).
Параметры панели MANAGE: общее количество шагов (Nsteps), через какое число шагов происходит остановка (N_fini), через сколько шагов выводится изображение (Speed), задержка после любого шага delay в миллисекундах (поставьте значение 500, и программа будет делать лишь два шага в секунду), и последнее: (*_) = коэффициент домножения графика на экране. Если он равен 100, то значение ординаты совпадает со значением на экране 1 - 2.8.
Кнопки обозначенные "<>" означают увеличение или уменьшение или увеличение данной величины (коэффициента, начальной амплитуды) на 1.1 или 1.01. "-" - изменение знака.
Справа внизу - суммарный график всех y от числа шагов (времени, t). Слева внизу текущие (первые 30) значения y,
Для самостоятельной работы, если хотите найти свой, "новый" солитон, нужно нажать на какой-то "Hit" (выбрать приблизительные условия), а потом изменить коэффициенты a, b, с (значками "-", "<", ">", "D=0" (эта кнопка делает данный коэффициент таким, чтобы дискриминант стал равен 0).
Потом выбрать начальные условия. Для этого выбираем нужные параметры и нажимаем кнопку "DO". (Кнопка "Add" под ней не делает, как кнопка DO, вначале, все значения равными 0, а только добавляет выбранное). И запускаем программу. Смотрим, что получилось...

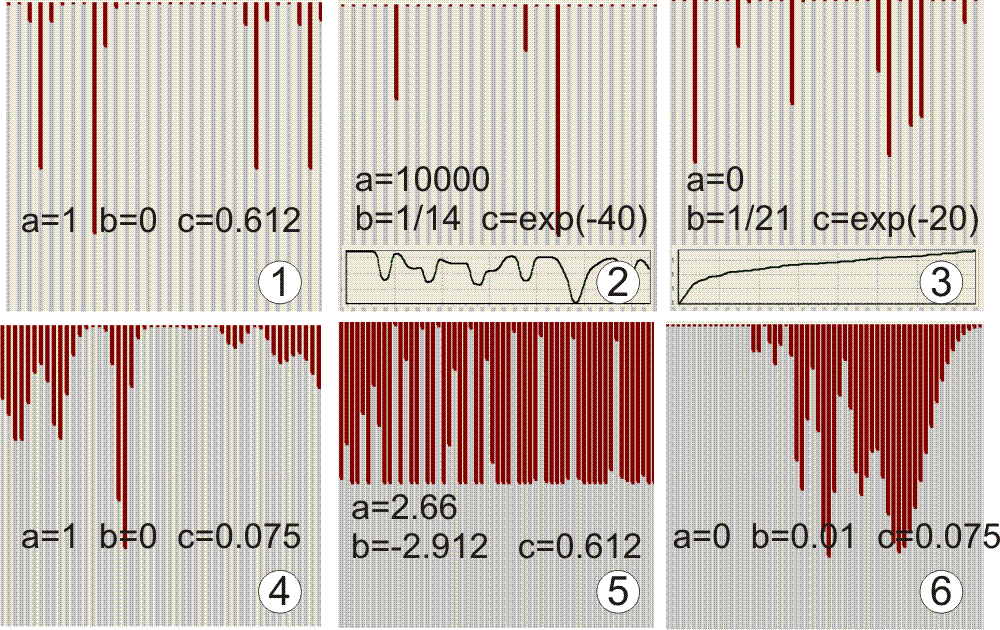
Рис. 2. Шесть примеров
работы программы.
Разберём кратко все наши кнопки "Hit".
I. Очень интересный пример самофокусировки. Кластер из трети (первых 10 из 30) первоначальных случайных значений переходят в 2 - 4 четыре, совершенно одинаковых, сфокусированных пучка. Каждый пучок через три шага повторяется, но смещается на две позиции вправо. Рис 2.1.
II. Солитонные Палочки без(!) Закона Сохранения. (Говорим что Закон Сохранения существует, если сумма всех y(t) приблизительно постоянна). "Солитонные Палочки" появляются прямо "из нуля", смещаясь при этом на одну позицию. Как водится, скорость движения Палочки возрастает с амплитудой. Палочки проходят друг через друга... но всего лишь несколько раз. (Каждый раз, при проходе, обе амплитуды слегка подравниваются. А когда они сравняются, Палочки идут уже синхронно). Рис 2.2.
III. Две солитонные Палочки с Законом Сохранения. (По моему мнению, это и есть первичный солитон). Если их амплитуды отличаются не сильно, то та которая по- больше не может перепрыгнуть ту которую по- меньше, и они так и идут, одна за другой. (А меняется ли, скорость первой палочки, когда её подгоняют? Догадайтесь... Ответ: "нет", не меняется! Она как шла, так и идёт, шаг в шаг! Нажмите сначала в кнопку "t1", а потом кнопку "t2" и убедитесь. (Надо будет подождать немножко, пока Палочка не достигнет координаты n=25).
IV. Шесть разных (существенно отличающихся по амплитуде) Палочек с Законом Сохранения. Палочка амплитуды 2 может проходить через Палочку амплитуды 1 сотни и сотни раз без существенного изменения амплитуд. Рис 2.3. Панель А[6] здесь же даёт шесть максимальных амплитуд, если брать три точки подряд. (Сначала определяется максимальная амплитуда. Потом эти точки выкидываются, и берутся три следующие... и так далее). Позволяет проследить, как "маленькие" солитоны "давятся большими".
Кнопка "s" ещё сначала сглаживает наши палочки. Это приводит к тому, что самая большая палочка начинает буквально "носится" по полю, перепрыгивая через другие солитоны.
V. Аналог КдФ уравнения. Хорошо вино, что оно, всё-таки, вторично по отношению к нашей Палочке из предыдущего пункта. Рис 2.4.
VI. Темновые "нестабильные" солитоны. Рис 2.5. Кнопки "+" и "-" дают по два два "чистых" тёмновых солитона. (Чтобы показать их прохождение друг сквозь друга). Особенно интересен второй случай! Тёмновой, отрицательный" солитон. Идёт в ДРУГУЮ СТОРОНУ!!! И тоже, естественно, проходит "друг сквозь друга"!
VII. Те же "темновые солитоны", но с очень быстрым остыванием.
VIII. Солитоны с разными амплитудами, идут с практически равными скоростями. (Солитонные пакеты). Рис 2.6.
Меняйте в программе коэффициенты a, b.с, параметры, выбирайте другие начальные условия и ищите новые солитоны. Странно, что я не встретил буквально- ТАКОГО солитона в литературе. Даже в энциклопедии [1] его нет? Что странно! "Палочка с Законом Сохранения" - по моему, очень красивая и интересная вещь.
Подменю главного меню "Exploring part" позволяет сделать постоянную подложку (для темновых солитонов), и сгладить наши y-ки. Один или сто раз.
Особая часть: Японские клеточные солитоны. (Я их назвал так, потому что их первыми исследовали японские математики[3]. По другому их называют "Система Ящиков Шаров". В ней шары сначала нумеруются по возрастанию (слева на право), а потом перекладываются: каждый на ПЕРВОЕ СВОБОДНОЕ место справа.
Выберите в главном меню Jap. works -> Have cell. solitons -> Go
Можете изменять
начальные параметры. Щелчок мышью на поле изменяет
состояние в данном месте на противоположное. Ставит-
убирает шар.
Литература:
[1] Энциклопедия Интегрируемых Систем. 2007, 2008 Институт Теоретической Физики. Редакция: А. Б. Шабат и другие...
[2] Дж. Л. Лэм. Введение в теорию солитонов. Москва "Мир" 1983
[3] J Phys Soc Japan
59 (1990), 3514–3519] D.Takahashi and J.Satsuma.
A Soliton Cellular Automaton.
J.Phys.Soc.Jpn.59
(1990)3514–3519