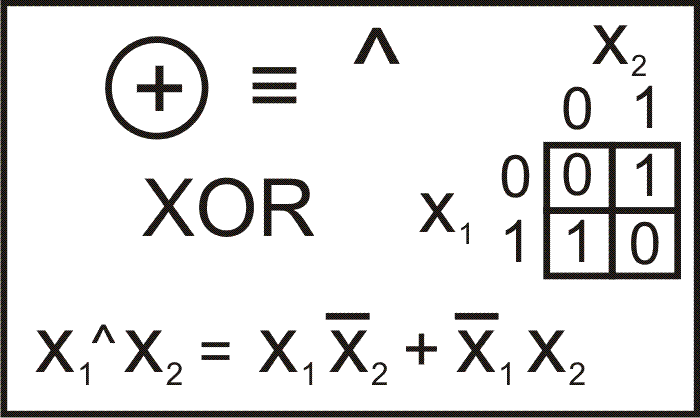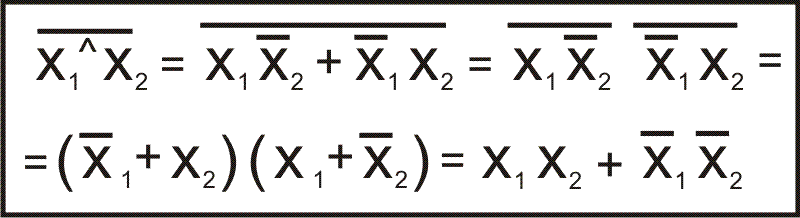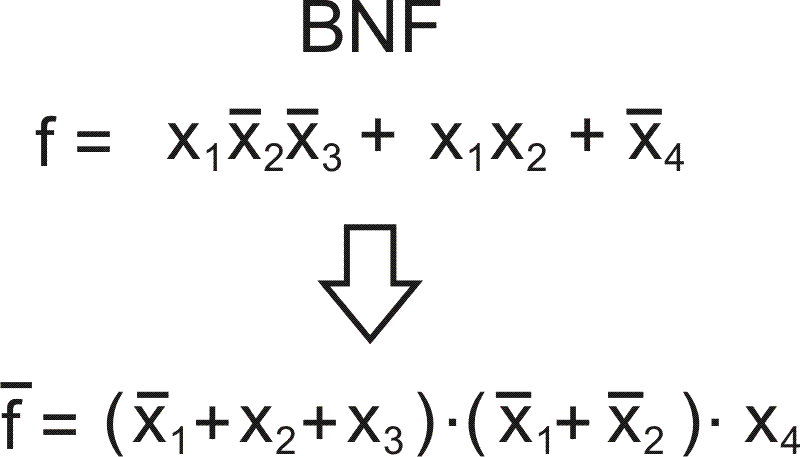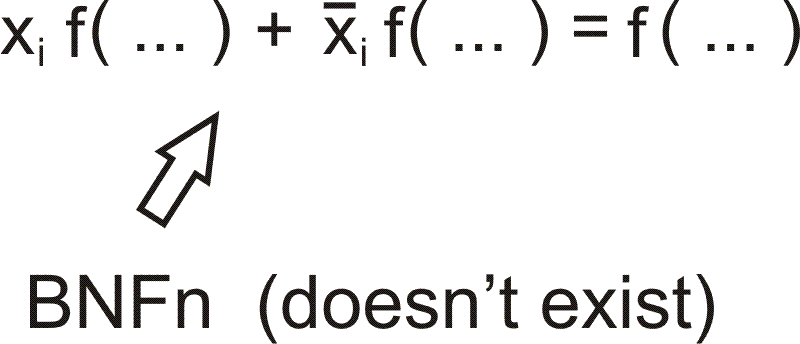Каждый большой учёный должен быть немного
извращенцем!
Алан Тьюринг
Лекции по "НОВОЙ" дискретной математике (начало)
1. Три проблемы которыми занимается НОВАЯ дискретная
математика.
Рассмотрим ТРИ основные вопроса над которыми думает
сегодняшняя наука:
Первый вопрос: что такое Жизнь или, слегка перефразируя, Как
Работает Рибосома?
Второй вопрос. Что же делать с перенормировками; вопрос об
основаниях Теории Поля.
И третий вопрос: как создать искусственный интеллект?
И вот как раз этими вопросами и занимается наша новая наука.
НОВАЯ дискретная математика.
Да!.. СТАРАЯ дискретная математика, хотя и пересекается - немного
- с НОВОЙ, нас совершенно не интересует! Ломать голову над
ерундовой P-NP проблемой, слегка улучшать никому не нужные
алгоритмы - это не наш путь! Меня, как и парапсиха, интересуют
только вечные вопросы.
Сиречь 3 вышеназванных. С той лишь разницей, что я ОТНЮДЬ НЕ
ПАРАПСИХ! И просьба меня с этими ушлёпками не путать!
2. О
рибосоме?
Существует БОЛЬШОЕ- БОЛЬШОЕ, просто КАТАСТРОФИЧЕСКОЕ недопонимание. Недопонимание -
МОЁ и связано вот с каким вопросом...
Предположим, что в телестудию на научно-популярную программу
пришёл Биофизик, и Телеведущий задаёт ему вопрос: объясните нам,
народу, популярно, что такое Жизнь. А в студии ещё сижу и я!
Независимый Наблюдатель. С правом совещательного голоса.
"Он" бы (телеведущий) - так и попросил! Но я бы, слегка,
уточнил... Вот, сказал бы я: стоит компьютер. Объясните мне,
популярно, как он может раз... и размножится! Воспроизвести самого
себя?? И ещё, очень важное замечание...
Здесь, на самом деле, есть ДВА,
СОВЕРШЕННО
РАЗНЫХ
вопроса!
Первый вопрос - данный!
И второй вопрос: как ещё могло получится, что такой
"сверх-экстравагантный" компьютер ещё и возник, вот так вот...
просто, из пустоты?
Просьба этого, второго, вопроса вообще
не касаться! Забыть о нём! Говорить только о первом. А мы
будем слушать! И со всем вниманием, напряжённо следить, что
Биофизик будет пытаться нам впарить...
Он говорит, что существуют ГЕНЫ. Двойная спираль из аминокислот.
("Очень интересно"???!!! Разумеется ЕСТЬ!! Ещё интереснее было бы, если бы ИХ НЕ
БЫЛО!!!???.. Вот это был бы номер!) Разумеется!.. Если есть
"компьютер", то должны быть, разумеется, и "программы"! ДНК - это
программы. И они, как собственно любой soft, очень легко
реплицируются, то есть копируются. Сначала к аминокислотам
прилипают их "анти", а потом они, всё вместе, расстёгиваются по
типу обычной застёжки "молнии". На штанах или на курках. Пока всё
хорошо и понятно...
... итак, представили! Повсюду плавают эти программы, эти самые
ДНК.
А дальше... Биофизик говорит, что существует такая штука - рибосома. И когда
определённая ДНК к ней подплывает, она её "захватывает" и
начинает, по её коду, воспроизводить определённый белок. Белок -
это "бусинки", которые потом складываются в трёхмерную структуру.
ОЧЕНЬ СЛОЖНУЮ! Сама по себе рибосома. состоит ~ из 60 разных макромолекул- белков...
То есть, на самом деле, рибосома - это такой мини заводик, который
может произвести что угодно!.." "А для чего нужен белок? Что он умеет
делать?" ...
Следует долгая тирада, смысл которой... что "доподлинно это
неизвестно, но кажется - ВСЁ!"
Ладно, согласимся и с этим!
Рибосома умеет производить "всё", в том числе, и себя саму! (Как
она это делает? Сначала выпускает 60 частей, которые потом сами
собой собираются?.. или пытается громоздить себя "всю сразу" - не
понятно! Но это не главное...) ГЛАВНОЕ, что рибосома., по словам
Биофизика,
НЕ СЛИЧАЕТ
того что она производит с САМОЙ СОБОЙ. "Есть программа - она
выдала белок".
А теперь я задаю вопрос: почему, в таком случае, никто и никогда не нарисовал
мультик -
КАК рибосома ЭТО ДЕЛАЕТ?
Выбрали бы себе такой ракурс с которого была бы видна и сама
"часть" и то как она... "собирается на стапеле"... "выходит из
заводских ворот"... не знаю! Ну, чтобы было видно, что это ТА ЖЕ
САМАЯ ЧАСТЬ. И нарисовали бы что- нибудь, научно- популярное!
Сейчас рисуют чудесные н.п. мультики! Одних Больших Взрывов я
наверное штук двадцать видел. Динозавры изумительные. (Другое
дело, что они, в большинстве - неправильные. Они, оказывается,
перьями были покрыты. Но это ерунда...)
Так я вам скажу, почему его никто не нарисовал? Потому, это его
НЕВОЗМОЖНО изобразить так, чтобы было НЕ СМЕШНО. И Вы, господин
Биофизик, сейчас несёте полную- не полную, но ДИЧЬ! И, по большому
счёту, НИ-ЧЕР-ТА не разобрались в том, что такое "жизнь"!..
"Согласен!!.. Есть
макромолекулы!.. они маленькие... разглядеть трудно! Что делать??!
Работаем, как можем!.."
Так ответил
бы мне
на это умный Биофизик
Ну а глупый, посмотрел бы
на меня печальными глазами и вежливо начал: "Извините! Но Вы ведь
ни черта не понимаете в химии..." На что бы я, в тон ему возразил:
"А зато у Вас, по моему мнению, вообще
нет мозгов!!" И до той поры пока бы меня не вывели
из студии, я никому бы не дал ничего говорить, и всё время
повторял: "где мультик??", "где мультик??", "где
мультик??"...
Такая вот у нас получилась бы беседа...
Мы в самом конце лекции попытаемся, тоже, что-нибудь вякнуть на
эту тему. Что говорит об этом НОВАЯ дискретная математика. Но,
тоже... получится не очень!
3. Что делать с
перенормировками?
Перейдём от проблем макромолекул к проблемам Теории Поля.
Есть такая наука Теория Поля и такая проблема – «проблема
перенормировок»!
Что это значит? А то, что в Теории Поля все ряды расходятся! Физики-
теоретики научились с ними работать. Обводят такой-то расходящийся
ряд… говорят, что это теперь «масса электрона»… и идут дальше! Но
так же делать нельзя! А «как надо» – никто не знает! Поле на
маленьких расстояниях начинает квантоваться. То есть переходит «на
поле… Дискретной Математики! А она – в том виде в котором
существуют – теор- физикам не помощник.
Так правильный ответ: так надо переходить на
поле не СТАРОЙ Дискретной Математики, а на поле НОВОЙ. Которая
вся (за исключением следующей главы) состоит из Автомата Чистой Тройки.
Потому что это ЕДИНСТВЕННОЕ интересное, что есть в ноликах и
единичках! Короче, читайте статью
4. Как сделать "искусственный интеллект"?
И
последняя проблема касается искусственного интеллекта.Известный
английский математик и гомосексуалист Алан Тьюринг, зверски замученный
британским правительством...
Да,
кстати, знаете эту историю?
Жил был такой Алан Тьюринг. Во
время последней войны он какие-то там немецкие шифры
расшифровал, благодаря чему (говорят!) Британия и
выиграла войну. А потом, уже в мирное время, внезапно
выяснилось, что он гомосексуалист. Британцы его, конечно, тут
же кастрировали (закон - есть закон!), а он, бедолага,
где-то через год, с тоски, выпил цианистого калия. В своё
время вся эта история наделала много шума. Алан Тьюринг стал,
своего рода, знаменем ЛБГТ движения, С него го всё и пошло...
Если не знаете, прочтите обязательно! Совершенно
душераздирающая история!!
(... НЕТ??? Вот так, сидишь себе дома, и вдруг - стук в дверь.
Заходят какие-то хмыри. Говорят, что они от "её Императорского
Высочества"... А потом связывают, и начинают резать член!..
Да, нет! С собой бы я, конечно, не покончил. Я уже человек в
годах, и член мне вроде- как не особо то и нужен. Но в любом
случае?!.. Если бы я, перед этим, ещё и спас свою державу в
Великой войне, то от подобного проявления благодарности, у
мене, безусловно, одна мозга зашла за другую, и я не знаю, чем
бы дело кончилось!..)
Так вот, этот самый Тьюринг придумал такой тест: на то умеет
ли машина думать или нет?
Это: сидите Вы и задаёте вопросы кому-то за шторкой. Если за 5
минут вы не сможете определить, кто вам отвечает компьютер или
человек, и отвечал вам компьютер, то это значит, что компьютер
тест прошёл!
Это несколько замысловатое определение. Мы придумали
определение по проще!
Искусственный интеллект: это "умение по виду результата работы",
догадаться (выписать) программу, которая бы этот результат получила. По видимому, эти определения
эквивалентны! Но, в любом случае, и та и другая проблема ещё
БЕСКОНЕЧНО далека от решения современной наукой.
Для НОВОЙ Дискретной Математики понадобится немножко СТАРОЙ.
Давайте коротко отметим, что там к чему.
4.1 Функции
NOT, AND, OR
Дискретная математика работает с одной переменной, которая
принимает два значения: 0 и 1.
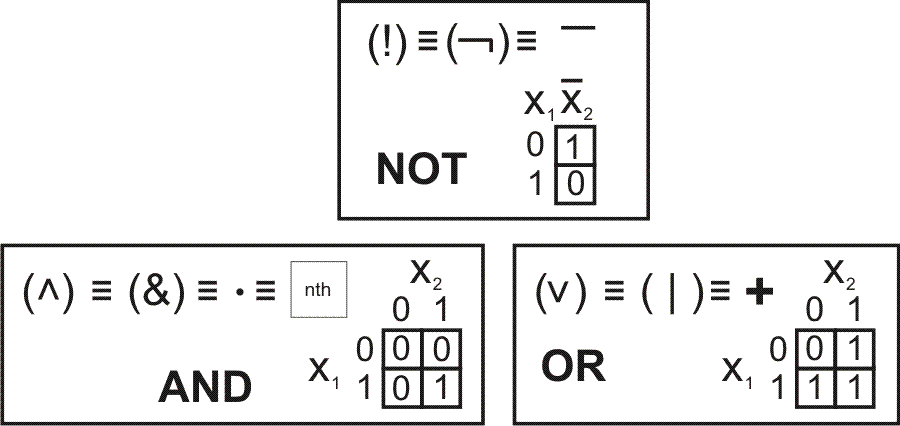
Имеется одна унарная (работающая с одной переменной) операция "НЕ"
("NOT"). И две бинарные (работающая с двумя переменными) операции "И"
("AND") и "ИЛИ" ("OR").
Показано на
рисунке. (Изображены все применяемые обозначения для них). Мы
будем применять для операции отрицания "черту сверху". Для
операции "ИЛИ" значок "+". А для операции "И" значок "вообще без
значка" (или точку; значок "умножить").
4.2 Функция "XOR"
Имеется ещё
одна очень важная бинарная операция "ИСКЛЮЧАЮЩАЯ ИЛИ" ("XOR") .
Операция транзитивна. То есть в выражении X1^X2^X3...
скобки расставлять не надо. (Функция XOR подсчитывает полное
количество единиц в Xi ; если оно чётно XOR = 0. В
другом случае XOR = 1).
Функция XOR "обратима" в том смысле, что X1^X1^X2 = X2.
То есть повторное применение оставляет выражение прежним.
4.3 Булева
функция, булева нормальная форма и булевы формулы. Формула де
Моргана.
Если для любой набора из n чисел 0 или 1 ставится 0 или 1, будем
говорить, что задана булева функция.
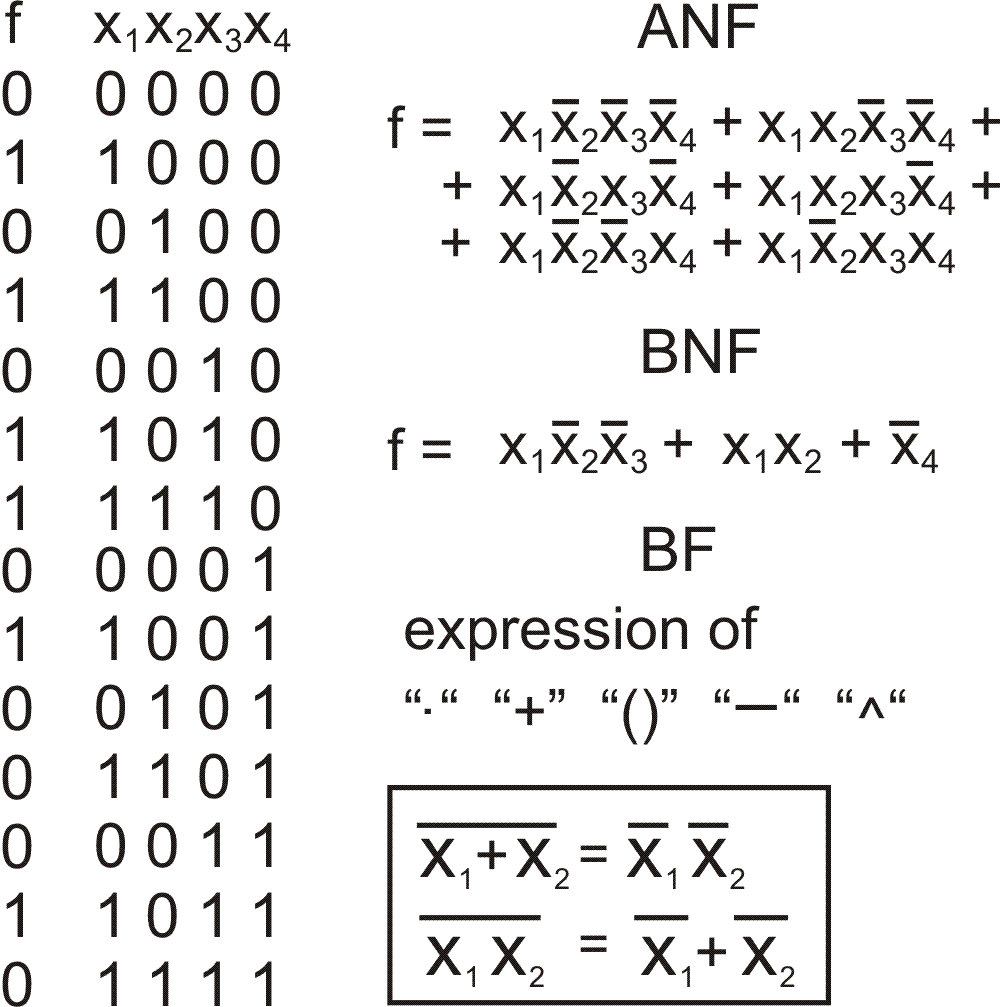
Её легко представить в виде таблицы. (Слева на рисунке).
Если мы выпишем все единички булевой формулы через знак сложения,
то получим так называемую Алгебраическую
Нормальную Форму (ANF).
Если в
этой формуле будут слагаемые раной длинны, назовём это выражение Булевой Нормальную Формой
(BNF)..
Любое выражение составленное из скобок и наших значков назовём булевой формулой (BF). (Выберем
последовательность действий в любой формуле. Сначала выполняется
действие умножения, потом операцию XOR, а затем операцию
сложения).
Любая булева функция легко превращается в в BNF путём обычных
правил сложения, умножения и формул де Моргана (на рисунке в
рамке). Пример на следующем рисунке.
4.4 Полином
Жегалкина.
Если взять дополнение (отрицание) к любой BNF мы, с помощью формул
де Моргана, получим другое выражение, в котором значки умножения и
сложения поменяются местами.
Но можно привести ещё одну формулу. А именно...
Любую Алгебраическую
Нормальную Форму можно однозначным образом перевести в другую
алгебраическую форму но в которой знаки сложения (" + ") заменены
знаком XOR (" ^ "). В так называемый "полином Жегалкина".
Если повторить это преобразование, то мы придём... к
первоначальной Алгебраической форме!
Я написал небольшую демонстрационную программку по этому поводу.
(Нажмите на изображение чтобы скачать
программу).
Измените любую "синюю" цифру и нажмите "Маке Zhegalkin
polynomial". Программа построит полином т.н. "методом
треугольника". Убедитесь в том, что мы сказали чуть ранее, что G2=E.
(Кнопка f=G(f)).
4.5 Алгоритм
Куэйна.
Если в BNF
какой-то функции находятся два такие члена
то такую функцию можно сократить.
Будем называть нормальной (BNFn) такую BNF в которой сделать это
нельзя. С первого взгляда не очевидное утверждение... для
некоторых булевых функций существует ГРАНДИОЗНОЕ количество разных BNFn! Легко убедимся в
этом...
Поставим проблему "симметризации" нашей булевой функции. Получить
из полной таблицы (ANF) минимальную
BNFn. (BNFn с минимальным количеством слагаемых).
В двадцатых годах прошлого века некий Куэйн предложил не хитрый
алгоритм, как это делать. Начинаем с ANF и говорим что все его
члены - импликанты 0-го уровня. После этого делаем первое
слияние, как на рисунке. Главное не торопиться! (А то вычеркнем
какой-то член, а он для другого слияния нужен!) То есть сначала
помечаем все слияния. Потом одновременно делаем сложения и
получаем импликанты первого уровня. Потом второго и так далее.
когда сокращать уже нечего - останавливаемся. Имеется
демонстрационная программа.
(Нажмите на изображение чтобы скачать
программу).
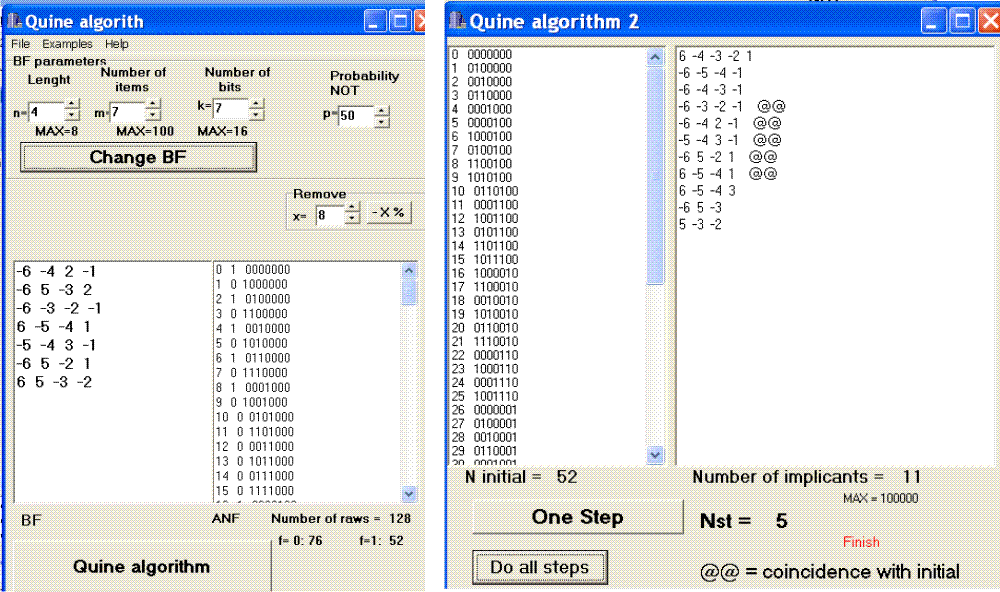
Кнопка
"Change BF" выбирает случайным образом нашу BNF. Дальше нажимаете
"Quine algorithm", и, на другой форме, кнопку "Do all steps". Как
видите на рисунке, из 7 слагаемых алгоритм правильно угадал лишь
5. (Иллюстрация неоднозначности BNFn).
(Первоначальные данные можете задать вручную в файле
bf.dat. Если в BNF имеется величина Xi
то обозначаем её i, если "НЕ" Xi
обозначаем её -i. Строка - одно слагаемое. (В
файле разделяются буквой "Q").
Очень интересно проследить слияние по шагам. Число импликантов
сначала резко возрастает (как С из n по k), а потом уменьшается.
Можно вычеркнуть сколько-то процентов из данных, и убедится, что
в этом случае алгоритм не работает вообще! Что понятно.
Выберите в качестве начальных данных Main menu -> Examples
-> Full resolving и увидите пример точной расшифровки).
4.6
Упорядоченная
бинарная
диаграмма
решений
(УБДР). (oBDD;
Odered Binary
Decission
Diagrams).
Как
мы видели для
любой булевой
функции может
существовать
много BNFn.
Но если
упорядочить нашу последовательностиданных, то мы придём, напротив
к однозначной записи
нашей булевой функции в виде т.н. УБРД.
Для этого, мы в два этапа....
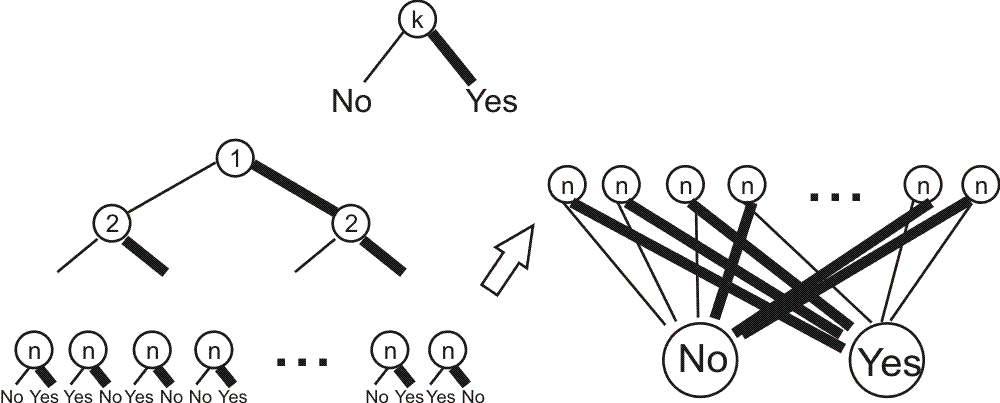
Сначала распишем нашу булеву функцию в виде т.н. полного дерева.
Потом объединим все ответы на последний вопрос в два кружка No и
Yes.
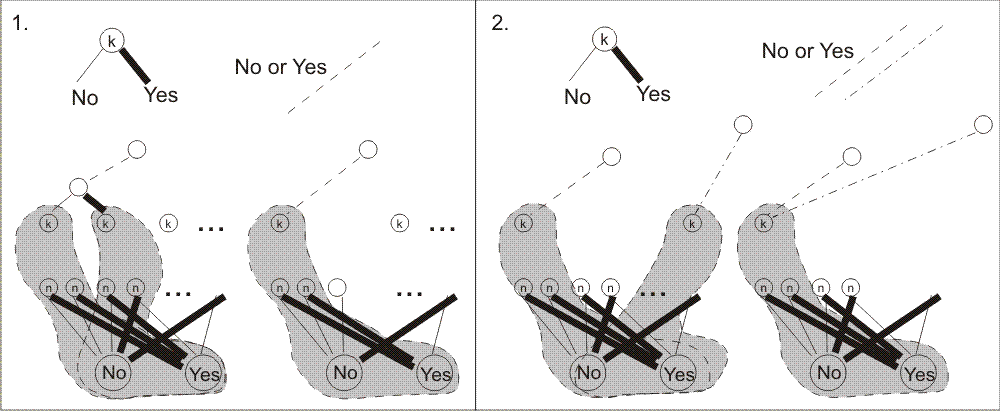
А теперь берём и ищем в дереве одинаковые (изоморфные) части.
Которые идут из каких-то двух вершин до самого конца. И легко видно, что в таком
случае можно одну из них вычеркнуть соответственно переставив одну
ветвь. (Показано на рисунке. Серым цветом мы показываем эти равные
части). Всего существует два разных вида "вычёркивания".
И легко показать, что эти простые правила приводят к однозначной
(УБДР).
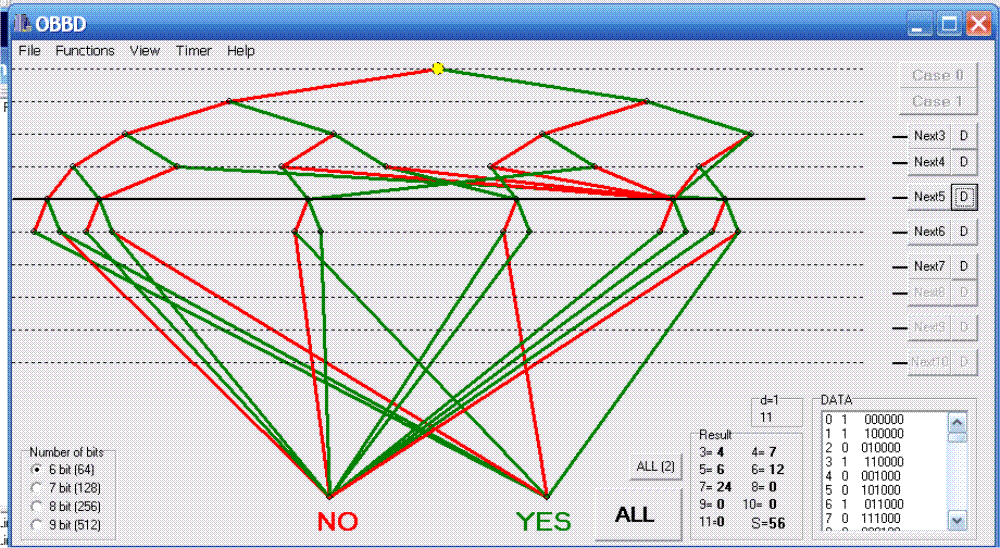
(Нажмите на изображение чтобы скачать
программу).
(Продолжение следует)